Kuanbing Caozhu*, Xiujun Yang and Changfa Ji
Xi'an University of Science and Technology, Xi'an, China
*Corresponding Author: Kuanbing Caozhu, Xi'an University of Science and Technology, Xi'an, China.
Received: February 15, 2021; Published: February 27, 2021
<The wall materials of the microcapsules affect the heat storage process of the phase change material in microcapsules with a plate. In this paper, Fluent CFD software is used and solidification/melting model is chosen to carry out the simulation of the heat storage process of the phase change material in microcapsules under the condition of four different wall materials of microcapsules. The physical model of the phase change microcapsules with equal spacing in combination with a plate is established and the liquid volume fraction and average temperature of the phase change material in microcapsules with time are analyzed. It can be concluded that when the phase change material is pure paraffin and its initial temperature is 324.15K, through the comparison of the liquid volume fraction of the phase change material in the process of phase change and the calculation of the heat storage capacity of phase change, it is concluded that when the wall material of microcapsules is urea formaldehyde resin, the amount of heat absorbed by the phase change material in the process of phase change is the most enormous, which is 7891.60901J. Thus, the urea formaldehyde resin is chosen as the most suitable wall material of microcapsule.
Keywords: Wall Materials; Microcapsules; Heat Storage Process; Phase Change Material
Phase change energy storage, also called latent heat energy storage, is a kind of energy technology in which the material absorbs latent heat to achieve heat storage when the phase of it changes. Phase change energy storage has the prospect of wide application in energy engineering, especially in solar heat storage, power grid load regulation day and night, the supply of heat in buildings and so forth [1]. Phase change materials used for energy storage have proper phase change temperature and larger phase change latent heat. Nevertheless, traditional phase change materials have disadvantages of poor performance of thermal conductivity, easy corrosion and so forth. These shortcomings can be compensated when the microencapsulation technology is introduced. After the microencapsulation of phase change materials, its heat transfer area increases [2]. Phase change material microcapsules can be used in wide areas, especially in thermal storage of buildings. They can be combined with concrete or sealed in the inner core of common building materials such as interior wall, floor, ceiling and so forth [3]. Phase change energy storage technology can be classified into phase change cold storage technology and phase change heat storage technology, so phase change energy storage materials possess the functions of heat storage and heat dissipation. With regards to the research on the heat transfer performance of phase change material microcapsules, specific work performed by scholars at home and abroad is as follows.
Through numerical simulation, Han., et al. analyzed the heat storage and heat release performance of phase change material microcapsules with multi cavity structure, the conclusion of which is that the more enormous the number of cavity is, the better its heat release performance is [4]; Zhao Yimeng., et al. conducted the research on the melting heat transfer of single phase change material microcapsules through numerical simulation with the method of sensible heat capacity and concluded that the thickness of capsule wall, the thermal conductivity of capsule wall, the particle size of microcapsules and other factors can affect the phase change heat transfer process of single phase change material microcapsules [5]; Dai Xiaoli., et al. carried out the research on the solidification heat transfer process in spherical phase change microcapsule through numerical simulation with the method of sensible heat capacity, made the analysis of its heat transfer performance and drew the conclusion that the volume change of phase change material exerts no apparent effect on the solidification process in the initial stage. However, the gradual increase in the ratio of solid phase of phase change material will weaken the heat transfer performance [6]; Jin Jian., et al. performed the study on the flow and heat transfer characteristics of latent heat fluid in a smooth pipe and a circular tube with an embedded coaxial cylinder by doing the numerical simulation. The results suggest that the flow of functional fluid in a circular tube with an embedded coaxial cylinder can improve the heat transfer performance. With the increase in the diameter of the embedded cylinder, the heat transfer effect is better. Nevertheless, in order to ensure that there is no large power consumption, the diameter of the embedded cylinder should not be too large [7].
According to the work done by scholars, the effect of microcapsule wall materials on the heat transfer process of phase change materials in microcapsules is seldom studied. In this paper, the research on the effect of microcapsule wall materials on the heat storage process of phase change materials in microcapsules combined with heat storage unit will be conducted.
Establishment of physical model and mathematics model Physical modelAs shown in figure 1, the length and width of the heat storage unit in combination with phase change material microcapsules are 250 mm and 200 mm respectively. The x-axis direction is the length direction of the heat storage unit, and the y-axis direction is the width direction of the heat storage unit. Microcapsules are spherical microcapsules and arranged with equal spacing. The size of microcapsules is fixed. The inner diameter of the capsule is 1 mm and the outer diameter of the capsule is 1.6 mm. The heat exchange fluid flows in from the left side of the heat storage unit and flows out from the right side. The other surfaces of the plate can satisfy the isothermal boundary conditions. Temperature of the surfaces are stable, which are 300K.
Figure 1: Physical model of heat storage of the plate with phase change material microcapsules.
As for the heat storage of phase change materials, the basic assumptions are: (1) the phase change material is isotropic; (2) the physical parameters of the phase change material are constant; (3) the initial condition of the phase change material is solid and the initial temperature is constant; (4) the heat storage process of phase change is unsteady; (5) the radiant heat transfer is neglected; (6) the volume of the phase change material in microcapsules in the process of phase change keeps unchanged; (7) the outer wall of the microcapsules is not adiabatic.
The monomer model of phase change material microcapsules is shown in figure 2. The phase change material is filled in the center of microcapsule, and the microcapsule wall material is filled around the outer wall of microcapsule.

Figure 2: Simple diagram of phase change microcapsule before phase change.
Mathematics modelFor the heat transfer of phase change material in microcapsules is involved, phase change occurs in the process of heat transfer. The heat transfer of the phase change studied in this paper is the solid-liquid phase change heat transfer, therefore the solidification/melting model in Fluent CFD software is chosen. The ratio of liquid phase β is introduced to reflect the change of volume fraction of the phase change material in microcapsules in the process of phase change heat storage. When β=0, the process of phase change heat storage has not started. When β=1, the process of phase change heat storage comes to an end. When the solid and liquid phase of the phase change material exist at the same time, 0<β<1, which indicates that the process of phase change heat storage is in progress. In the course of phase change material from solid phase to liquid phase, transfer of latent heat exists. The governing equation of phase change heat transfer is non-linear equation. In this paper, the control volume method is employed to solve the problem of heat transfer of phase change materials. The crucial governing equations include continuity equation and energy conservation equation, which are as follows.
Continuity equationIn equation 1, ρ is density; u, v, w are the component velocity in the x, y and z axis direction.
Energy conservation equationIn equation 2, H is the total enthalpy; v is the fluid velocity, k is the thermal conductivity and S is the source term.
According to literature 8, the total enthalpy is the sum of sensible enthalpy and latent enthalpy, which is H=h+ΔH. And ΔH is the latent enthalpy and h is sensible enthalpy.
In equation 3, href is the reference enthalpy; Tref is the reference temperature, and cp is the specific heat capacity at constant pressure.
In equation 4, β is the ratio of liquid phase; and L is the latent heat of the phase change material.
When T < Tsolidus, β = 0, T > Tsolidus, β = 1, and Tsolidus, ≤ T ≤ TTliquidusT, β = (T-TTsolidusT)/(TTliquidusT-TTsolidusT). Thus, when the phase change material is solid phase, the total enthalpy H equals the sensible enthalpy h, when the phase change material is liquid phase, the total enthalpy is the sum of the sensible enthalpy and the latent heat of phase change material. In the process of phase change heat storage of phase change material, 0 < β < 1. The ratio of liquid phase is the linear function of temperature. For a specific phase change material, its latent heat is constant, thus the latent enthalpy ΔH is the linear function of temperature. In the heat storage of phase change material, the source term of the equation is not taken into account, thus S is 0.
Setting of boundary conditionsAfter the model is meshed, the mesh file is imported into the Fluent CFD solver. The solver is 3 dimensional, pressure based, transient, absolute velocity and segregated solver. The mesh is smoothed through the command “mesh---smooth/swap” in Fluent CFD software. For the closer the minimum orthogonal quality is to 0, the worse the mesh quality is. The minimum orthogonal quality can be improved through the command “mesh--smooth/swap” so that the purpose of improving mesh quality can be achieved. The solidification/melting model is used to conduct the simulation of the heat storage of phase change materials in microcapsules. The inlet velocity of heat transfer fluid is 0.01m/s, and the inlet temperature is 343K. When the velocity and pressure at the outlet are unknown, the outlet boundary condition can be set as the outflow boundary condition [9]. Except for the inlet and outlet of heat exchange fluid, the other surfaces are set as isothermal boundary condition, and the temperature is 300K. In order to improve the accuracy, the second order upwind scheme is employed to solve the energy equation. The pressure gradient adopts the Second Order scheme, the pressure-velocity coupling method is SIMPLE algorithm, and the relaxation factors are set by default. The initial values of parameters are set with the standard initialization method for the overall solution area. When the initial temperature is set, the initial temperature of microcapsule wall material is 343K, the initial temperature of phase change material in microcapsule is 324.15K, the initial temperature of heat exchange fluid--water is 343K, the time step is 1s, and the convergence criterion is that the residual error of the energy equation is less than 10-6. In this paper, the volume fraction of liquid phase in the phase change material region and the average temperature of the core material of microcapsules (phase change material) with time are monitored through the command “solve--monitor” in Fluent CFD software. The density, specific heat, latent heat, solidus temperature, liquidus temperature and thermal conductivity of paraffin are 760kg/m3, 2100[J/(K*kg)], 170kJ/kg, 324.15K, 330.15K and 0.25W/(m*K) respectively [10], the physical parameters of urea formaldehyde resin are shown in table 1 [8] and the physical parameters of polystyrene, polyvinyl alcohol and polyethylene are shown in table 2-4. The grid of higher quality is the key to gaining the accurate solution, so in order to make the results of numerical simulation more accurate, the orthogonal quality is improved through the command “mesh--smooth/swap” in Fluent CFD software so as to make the orthogonal quality much larger than 0. Indeed, the closer the orthogonal quality is to 0, the poorer the mesh quality is, and the further the orthogonal quality is to 0, the better. The mesh quality is improved by improving orthogonal quality, which can make the solution more accurate. At the same time, in order to improve the solution accuracy, the second order upwind scheme is employed to solve the energy equation, which is more accurate than the first order upwind scheme.
| Name | Density | Specific heat | Thermal conductivity |
|---|---|---|---|
|
Urea Formaldehyde Resin |
1420 |
1672 |
0.56 |
Table 1: Physical parameters of urea formaldehyde resin.
| Name | Density | Specific heat | Thermal conductivity |
|---|---|---|---|
|
Polystyrene |
1050 |
1300 |
0.08 |
Table 2: Physical parameters of polystyrene.
| Name | Density | Specific heat | Thermal conductivity |
|---|---|---|---|
|
Polyvinyl Alcohol |
1270 |
1000 |
0.2 |
Table 3: Physical parameters of polyvinyl alcohol.
| Name | Density | Specific heat | Thermal conductivity |
|---|---|---|---|
|
Polyethylene |
910 |
2218 |
0.35 |
Table 4: Physical parameters of polyethylene.
Analysis of numerical simulation resultsIn this paper, control variation method is employed to carry out research on the effect of microcapsule wall materials on the heat storage process of phase change materials in microcapsules. The initial conditions and boundary conditions are unchanged, so is the size of all microcapsules. The inner diameter of microcapsules is 1mm, the outer diameter of microcapsules is 1.6mm, and the pure paraffin is chosen as the phase change material, whose physical parameters are constant. In case 1, the wall material of microcapsules is urea formaldehyde resin, in case 2, the wall material of microcapsules is polystyrene, in case 3, the wall material of microcapsules is polyvinyl alcohol, and in case 4, the wall material of microcapsules is polyethylene. Figure 3 is the diagram of the liquid volume fraction of phase change material with time under four working conditions.
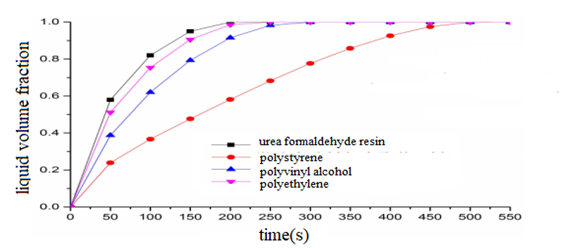
Figure 3: Variation graph of liquid volume fraction of phase change material.
It can be seen from figure 3 that under the four working conditions, the variation trend of liquid phase volume fraction of phase change materials is fast at first, and gradually tends to be stable as time goes on. When the liquid volume fraction of phase change material is close to 1, the diagrams of the liquid volume fraction of phase change material nearly coincide under the four working conditions. As is seen in figure 3, when the wall material of microcapsule is urea formaldehyde resin, the liquid volume fraction of phase change material is the largest and increases at a faster speed. When the wall material of microcapsule is polystyrene, the liquid phase volume fraction of phase change material is the smallest and increase more slowly. The thermal conductivity of four kinds of microcapsule wall materials is varied. Because the order of thermal conductivity is urea formaldehyde resin > polyethylene > polyvinyl alcohol > polystyrene, the liquid phase volume fraction of phase change material increases with the increase in the thermal conductivity of microcapsule wall materials. The shorter the time for the liquid volume fraction of phase change material to reach 1, the shorter the time for the phase change material to finish the melting process, and the faster the melting rate of the phase change material. For the phase change material absorbs heat when it is melting, with the increase in the thermal conductivity of microcapsule wall materials, the time for the phase change material to complete the heat storage of phase change is shorter.
The specific time when the liquid volume fraction of the phase change material reaches 1 cannot be seen clearly from figure 3. The time for the phase change material to finish the phase change heat storage under the four working conditions and the liquid phase volume fraction to reach 1 is shown in figure 4.
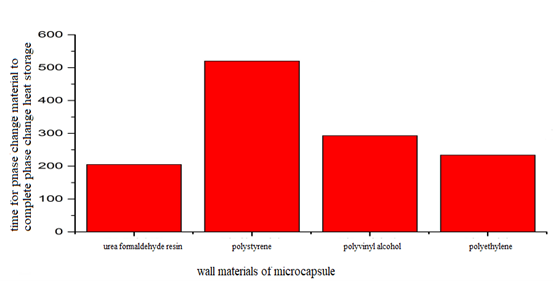
Figure 4: Time variation of phase change heat storage of the phase change material.
As the thermal conductivity is in the order of polystyrene In this paper, radiant heat transfer is not considered and it is assumed that the process of heat storage is carried out at night. At night, heat transfer fluid is heated with electricity to make its temperature higher than that of the phase change material, then the process of heat storage of the phase change material in microcapsules from the heat exchange fluid can be achieved. Under four working conditions, the average temperature variation of the phase change material in microcapsules is shown in figure 5. Figure 5: Average temperature of the phase change material in microcapsules in the process of heat storage. It can be seen from figure 5 that under the four working conditions, the average temperature of the phase change material in microcapsules increases at first and tends to be stable as time goes on. Varied wall materials of microcapsules have an apparent effect on the temperature of the phase change materials in microcapsules. When the wall material of microcapsule is urea formaldehyde resin, the average temperature of the phase change material in microcapsules rises at the fastest speed. When the wall material of microcapsule is polystyrene, the average temperature of the phase change material in microcapsules rises at the slowest speed. It is because when the wall material of microcapsules is urea formaldehyde resin, it takes the phase change material the shortest time to finish the melting and the process of the heat storage of phase change, therefore the rate of melting and heat storage is the fastest, and the temperature of the phase change material rises at the fastest speed. When the wall material of microcapsules is polystyrene, it takes the phase change material the longest time to finish the melting and the process of the heat storage of phase change, therefore the rate of melting and heat storage is the slowest, and the temperature of the phase change material rises at the slowest speed. Because the order of the thermal conductivity is urea formaldehyde resin > polyethylene > polyvinyl alcohol > polystyrene, when the wall material of the microcapsule is urea formaldehyde resin, the thermal conductivity is the largest. In accordance with the fact that the thermal resistance is equal to the wall thickness divided by the thermal conductivity, the thermal resistance is in inverse proportion to the thermal conductivity. Therefore when the wall material of microcapsules is urea formaldehyde resin, the thermal conductivity is the smallest. And because the exterior wall of microcapsules is not adiabatic, it is easier for the heat exchange fluid to transfer heat to the phase change material, the rate of the heat storage of the phase change material is faster, and its average temperature rises faster. According to the previous analysis, the phase change heat storage rate of the phase change material is urea formaldehyde resin > polyethylene > polyvinyl alcohol > polystyrene. It can be known from figure 5 that the faster the heat storage rate of phase change is, the faster the average temperature rises. As time goes by, the temperature of the phase change material tends to increase slowly. It is because the amount of heat absorbed by the phase change material is on the increase as time goes on, the heat storage capacity tends to be more saturated. And the ability to absorb heat is gradually on the decrease, and the rate of heat storage tends to be slower. Thus, the amount of heat absorbed by the phase change material tends to increase slowly, so does its average temperature.
The contours of liquid volume fraction of the phase change material of the plate with microcapsules z=0 with time under the four working conditions are displayed in figure 6. Figure 6: Contours of the liquid volume fraction of the phase change material. It can be seen from figure 6 that under the four working conditions, the phase change material in microcapsules has obvious phase change from time τ = 0s to time τ = 150s. When the wall material of microcapsules is urea formaldehyde resin, most of the areas in microcapsules have melted, and there are fewer areas that have not melted. When the wall material of microcapsules is polystyrene, the melting layer is the thinnest and the two phase zone of the solid-liquid is most obvious. It can be seen that the liquid volume fraction of the phase change material gradually decreases from the outside to the inside of each microcapsule. As time goes on, the solid-liquid two phase region of the phase change material gradually moves to the inner center of microcapsules. It can be found that the solid-liquid two phase region gradually shrinks when it moves to the inner part of the microcapsule, and the phase change material in the center of the microcapsule basically doesn’t melt.
Under the four working conditions, the amount of heat absorbed by the phase change material is different when different wall materials of microcapsules are chosen. According to the formula Q=M×(H2-H1), when the wall material of the microcapsules is urea formaldehyde resin, the amount of heat absorbed by the phase change material in the process of phase change, that is, the latent heat is 7891.60901J. Similarly, when the wall materials of the microcapsules are polystyrene, polyvinyl alcohol and polyethylene respectively, the amount of heat absorbed by the phase change material in the process of phase change is 7602.9711J, 7792.008J and 7851.202J. It can be seen that when the wall material of the microcapsules is urea formaldehyde resin, the amount of heat absorbed by the phase change material in the process of phase change is most enormous. Under the four working conditions, the mass and initial enthalpy of the phase change material are the same. Because when the wall material of the microcapsules is urea formaldehyde resin, it takes the shortest time for the liquid volume fraction of the phase change material to reach 1, the rate of phase change heat storage and the temperature rise at the fastest speed, the amount of heat storage of the phase change material in the process of phase change is largest. The order of the thermal conductivity is urea formaldehyde resin > polyethylene > polyvinyl alcohol > polystyrene, the rate of phase change heat storage and temperature rise at a fast speed with the increase in the thermal conductivity of the wall material of microcapsules. When the wall material of microcapsules is urea formaldehyde resin, the temperature of the phase change material in the process of phase change rises at the fastest speed. In the same period of time, the amount of heat absorbed by the phase change material is the largest, which indicates that the temperature of the heat exchange fluid is higher than that of the phase change material. It suggests that the amount of power used to heat exchange fluid and raise the temperature of heat exchange fluid can be reduced and the power consumption can be saved. Thus, the electricity price can be saved and the purpose of energy saving can be achieved.
In the paper, with the Fluent CFD simulation software, the research on the effect of different wall materials of microcapsules on the heat storage process of the phase change material in microcapsules is performed with the control variation method. Conclusions are as follows:
Citation: Kuanbing Caozhu., et al. “Research on the Effect of the Wall Materials of Microcapsules on the Heat Storage Process of the Phase Change
Material in Microcapsules".Acta Scientific Agriculture 5.3 (2021): 55-62. Copyright: © 2021 Kuanbing Caozhu., et al.This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.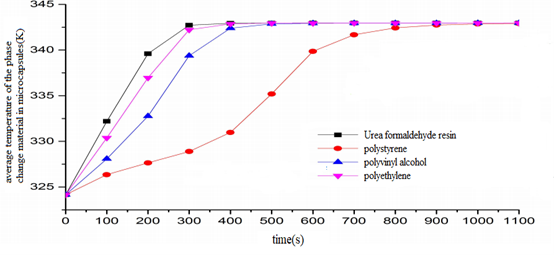
Conclusions
Bibliography
Citation
Copyright
ff
© 2024 Acta Scientific, All rights reserved.