James A Thompson*
College of Veterinary Medicine and Biomedical Science, Texas A&M University, USA
*Corresponding Author: James A Thompson, College of Veterinary Medicine and Biomedical Science, Texas A&M University, USA.
Received: September 09, 2020; Published: September 29, 2020
Citation: James A Thompson. “The Effects of Parent Ages on Birth Defects”. Acta Scientific Paediatrics 3.10 (2020):58-69.
Background: Men and women, in the United States, are having children at considerably older ages. This changing demographic has been associated with multiple neonatal adverse birth outcomes that are currently considered to constitute a major public health crisis. The objective of this study was to evaluate the risk of parent age on birth defects and to provide results that can serve as a starting point for more specific mediation modeling. The modeling estimated the effects of parent age on birth defects controlling for confounding between maternal and paternal age and separated the mediating effect of chromosomal disorders, including Down syndrome.
Methods: Data containing approximately 15,000,000 birth records were obtained from the United States Natality database for the years 2014 to 2018. A Bayesian modeling approach was used to estimate adjusted risks of parent ages both unadjusted and adjusted for the other parent’s age and for the mediational effect of chromosomal disorders, including Down syndrome.
Results: Increasing maternal age was associated with increased risks for hypospadias and cyanotic congenital heart disease. Increasing maternal and paternal ages were associated with decreasing risks for gastroschisis. For limb reduction defect, cleft lip and all defects combined, the risk of maternal age was U-shaped with the lowest risks observed at approximately age 35y. Paternal age was not associated with an increase in the birth prevalence of birth defects.
Conclusion: Advancing maternal age was associated with increased birth prevalence of hypospadias and cyanotic congenital heart disease and associated with a lower birth prevalence for gastroschisis. Both older and younger maternal ages were related to limb reduction defect and cleft lip. Advancing paternal age was not associated with an increased birth prevalence of birth defects but was associated with a decreased birth prevalence of gastroschisis.
Keywords: Bayesian; Birth Defects; Maternal Age; Paternal Age
CAR: Conditional Autoregressive; CD: Chromosomal Disorders, Excluding Down Syndrome; CD/DS: Chromosomal Disorders, Including Down Syndrome; DAG: Directed Acyclic Graph; DS: Down Syndrome; IRB: Institutional Review Board; MCMC: Markov Chain Monte Carlo; NVSS: National Vital Statistics System; OR: Odds Ratio
Men and women, in the United States, are having children at considerably older ages [1]. This changing demographic is thought to cause multiple adverse birth outcomes and a major public health crisis has resulted [2]. Much of the concern regarding advanced maternal age is the increased risk for meiotic nondisjunction in developing oocytes resulting in chromosomal disorders, including Down syndrome [3]. However, the role of maternal age in causing birth defects in the absence of maternal aneuploidy is controversial [4]. The major concern among men is that mitotic errors accumulate among spermatogonia contributing to increased germline mutations that are related to a collection of abnormal birth outcomes [5]. However, the empirical evidence that these mutations cause birth defects is controversial [6]. The most important difficulty implicating paternal age as a cause of neonatal adverse birth outcomes, in general, and birth defects, specifically, appears to be confounding by maternal age [6]. When modeling the joint effects of maternal and paternal ages, two approaches have predominated [7]. The linear or curvilinear (linear and quadratic) approach is usually inadequate because the functions will often fit well over specific age ranges and fit poorly over other age ranges. Dividing ages into categories has been preferred by many with 10-year age groups the most common approach but because of the very high correlation this approach is certain to leave residual confounding within categories [7]. Recently, it was shown that Bayesian modelling of joint maternal and paternal age effects with conditional autoregressive (CAR) priors provided a much superior fit for the risks of Down syndrome and other chromosomal disorders [8]. The novel approach measured age to the nearest year and facilitated smoothing of age-specific parental risk estimates to the risk estimates of ages one year younger and one year older as an autoregressive function. The modeling facilitated precise estimation of age-related risks that were non-linear. While joint conditioning of both parental ages is arbitrarily complex, it is straightforward under a Markov Chain Monte Carlo (MCMC) implementation. The objective of this study was to evaluate the risk of parent age on birth defects and to provide results that can serve as a starting point for more specific mediation modeling. The causal modeling will estimate the effects of parent age on birth defects controlling for confounding between maternal and paternal age and will separate the mediating effect of chromosomal disorders, including Down syndrome.
Data containing approximately 15,000,000 birth records were obtained from the United States Natality Database for the years 2014 to 2018. In the United States, state laws require birth certificates to be completed for all births, and federal law mandates national collection and publication of births and other vital statistics data. The National Vital Statistics System (NVSS), the federal compilation of these data, is the result of the cooperation between the National Center for Health Statistics (NCHS) and the states to provide access to statistical information from birth certificates. The fields retained for analysis included both parents’ ages, the presence of each of 10 monitored birth defects, Down syndrome and chromosomal disorders (other than Down syndrome). This study was evaluated by the Texas A&M Institutional Review Board (IRB) and determined to be exempt from IRB review.
Odds ratios (OR) for birth defects associated with Down syndrome (DS) and chromosomal disorders other than Down syndrome (CD) were estimated as follows: Data were cross tabulated for each of I = 2 levels (present/not present) for k = 11 birth defect classifications. For each row in the table, the count of cases at birth was tabulated as Yik and the count of births as ni. The case counts were modeled as independent Binomial distributions conditional on an unknown rate parameter (μik):
Yik ~ Binomial(μik,ni)
Each rate parameter (μik) was given a Uniform (0,1) prior. The odds ratios were estimated by converting the rate parameter to an odds and calculating the ratio of the odds:
ORk = [μ2,k/ (1 – μ2,k)] / [μ1,k / (1 – μ1,k)]
In order to estimate the unadjusted effect for maternal age, case counts for each of k=11 birth defect classifications were cross tabulated by i = 35 maternal ages (15 to 49 years). For each row in the table Yik was the count of cases, at birth, and ni, the count of births. The counts were modeled as independent Binomial distributions conditional on an unknown rate parameter (μik):
Yik ~ Binomial(μik,ni)
The logit of the rate parameter was then modeled as a linear function of the overall intercept and a random effect for each maternal age:
Logit(μik) = αk + maternalik
The intercept was given a flat, improper prior. The maternal prior was a minimally informative CAR or random walk prior of length 35 (ages (i) = 15 to 49). The precision of the CAR prior was specified as Uniform (0,10) on the standard deviation scale.
In order to estimate the unadjusted effect for paternal age, case counts for each of k = 11 birth defect classifications were cross tabulated by j = 51 paternal ages (15 to 65 years). For each row in the table, Yjk was the count of cases, at birth, and nj, the count of births. The counts were modeled as independent Binomial distributions conditional on an unknown rate parameter (μjk):
Yjk ~ Binomial(μjk,nj)
The logit of the rate parameter was then modeled as a linear function of the overall intercept and a random effect for paternal age:
Logit(μjk) = αk + paternaljk
The intercept was given a flat, improper prior. The maternal age prior was a minimally informative CAR or random walk prior of length 35 (ages (i) = 15 to 49) and the paternal age prior was a minimally informative CAR or random walk prior of length 51 (ages (j) = 15 to 65). The precision for the CAR priors was specified as Uniform (0,10) on the standard deviation scale.
In order to estimate the adjusted effect for maternal age, data were restricted to neonates who were negative for DS and CD. Case counts for each of k=11 birth defect classifications were cross tabulated by i = 35 maternal ages (15 to 49 years) and j = 51 paternal ages (15 to 65 years). For each row in the table Yijk was the count of cases, at birth, and nij, the count of births. The counts were modeled as independent Binomial distributions conditional on an unknown rate parameter (μijk):
Yijk ~ Binomial(μijk,nij)
The logit of the rate parameter was then modeled as a linear function of the overall intercept and a random effect for each maternal and paternal age:
Logit(μijk) = αk + maternalik + paternaljk
The intercept was given a flat, improper prior. The maternal age prior was a minimally informative CAR or random walk prior of length 35 (ages (i) = 15 to 49) and the paternal age prior was a minimally informative CAR or random walk prior of length.
51 (ages (j) = 15 to 65). The precision for the CAR priors was specified as Uniform (0,10) on the standard deviation scale.
In order to estimate the adjusted effect for paternal age, all data including data for neonates identified with DS and CD were used. While the data were different, the model to estimate the adjusted effect for paternal age was the same model as used to estimate the maternal age adjusted effect.
All age-related odds ratios were standardized to age 15. The implementation used MCMC and the software MultiBUGS 1.0.0 [9,10].
All parameters were estimated with each iteration of the Markov Chain. Five thousand iterations were allowed for burn-in and every hundredth of the next 200,000 iterations were collected for the posterior distribution. Convergence was determined by observing multiple chains with disparate starting values. Bayesian credible intervals were taken directly from the full posterior distributions. A significant age effect was defined as at least one age having a Bayesian posterior predictive p-value of < 0.05 [11]. A sensitivity analysis was performed for each parent age model by adjusting the rate parameter by dividing the rate parameter by possible sensitivities of the birth defect detection for sensitivities of 0.75, 0.5 and 0.25 and the estimation was repeated, and results compared.
The accessed data identified 15,077,411 singleton births during the study period.
Of these, 8,323 mothers were less than 15y of age and 2,492 were older than 49y.
Among fathers, 67,096 were younger than 15 y and 3,516 were older than 65 years. Father’s age was missing for 1,780,585 births which included births for which the father was not identified. There were 7,913 births for which both the mother’s age was out of the study’s age range and the father’s age was missing or out of the study’s age range. It was very common for mothers aged less than 15y for the father’s age to be missing (72%; 6008/8323). In total, 1,862,012 births were deleted for missing or out of range parent ages. Outcome variables were missing for 14,701 births and these births were deleted. In total, 13,207,486 births were used in the analyses.
Both Down syndrome and chromosomal disorders, other than Down syndrome were strongly related to all 10 monitored BD and all BD combined (Table 1).
The adjusted effect of increasing paternal age was not associated with increased risk of birth defects (Figures 1-11) but was associated with a decreased risk of gastroschisis to age 45y and then a relatively uniform risk to age 65y (Figure 4). The adjusted effect for increasing maternal age was associated with increased risk for hypospadias (Figure 2) and cyanotic congenital heart disease (Figure 3) and a decreased risk for gastroschisis (Figure 4). For gastroschisis, the odds ratio for maternal age 15y had an odds ratio (and 95% credibility interval) of 19.7 (7.9, 72.4) relative to age 49y.
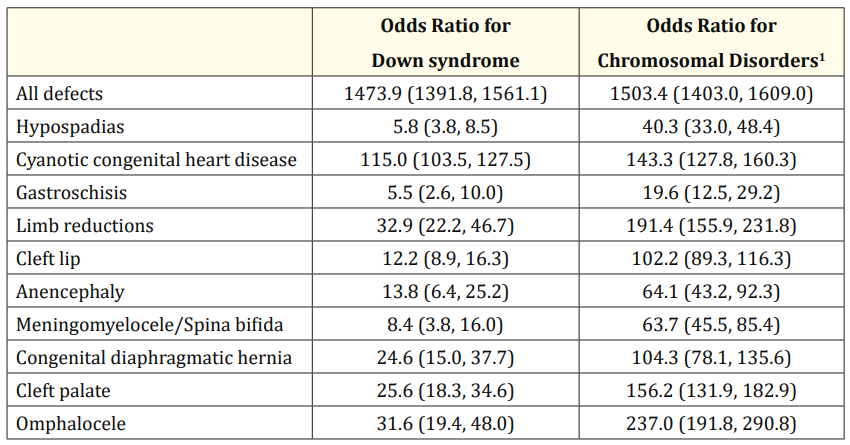
Table 1: Odds ratios (95% credibility interval) for Down syndrome and chromosomal disorders other than Down syndrome on birth defects.
1Chromosomal disorders other than Down syndrome.
For limb reduction defect (Figure 5), cleft lip (Figure 6) and all defects combined (Figure 1), the risk of maternal age was U-shaped with the lowest risks observed at approximately age 35y. Relative to age 35y, the odds ratio for maternal age 15y was 1.65 (1.16, 2.52), 1.25 (1.00, 1.53) and 1.30 (1.12, 1.50) for limb reduction defect, cleft lip and all defects combined, respectively. Relative to age 35y, the odds ratio for maternal age 49y was 1.47 (0.87, 2.89), 1.28 (0.97, 1.78) and 1.27 (1.05, 1.65) for limb reduction defect, cleft lip and all defects combined, respectively. Results of the sensitivity analysis showed that the model intercept was influenced by the choice of sensitivity, but the parent age odds ratios remained virtually identical.
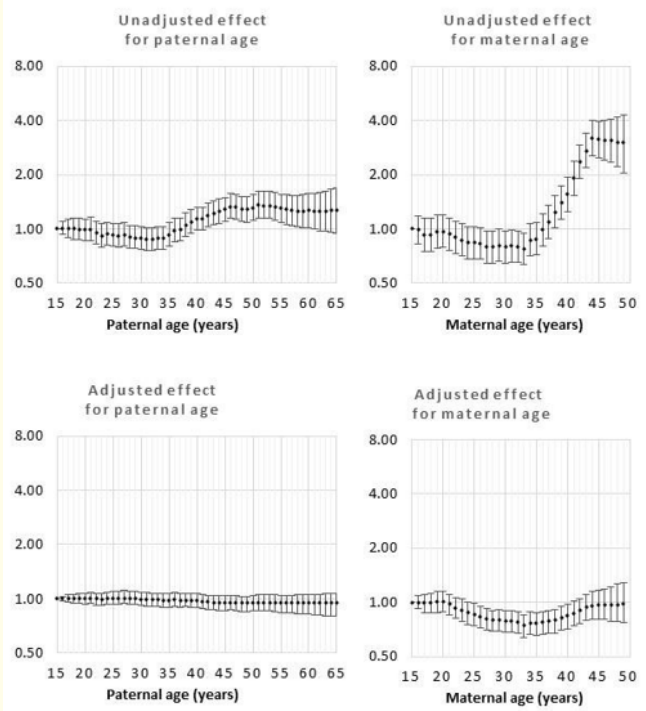
Figure 1: Odds rations for unadjusted and adjusted effects by parent age relative to age 15 years for all defects
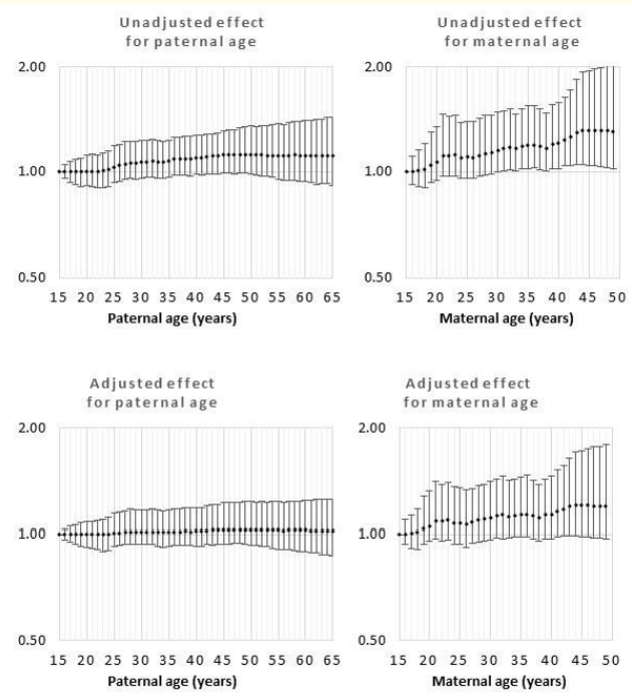
Figure 2: Odds rations for unadjusted and adjusted effects by parent age relative to age 15 years for Hypospadias.

Figure 3: Odds rations for unadjusted and adjusted effects by parent age relative to age 15 years for Cyanotic congenital heart condition.
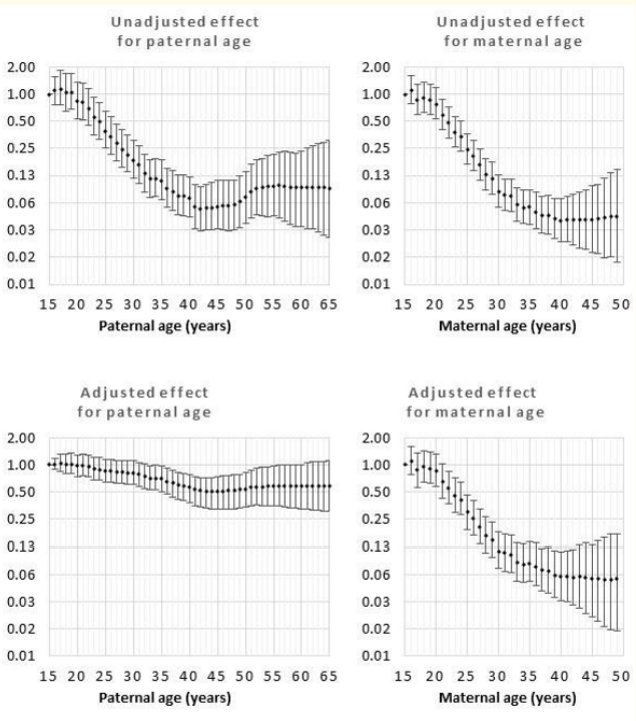
Figure 4: Odds rations for unadjusted and adjusted effects by parent age relative to age 15 years for gastroschisis.
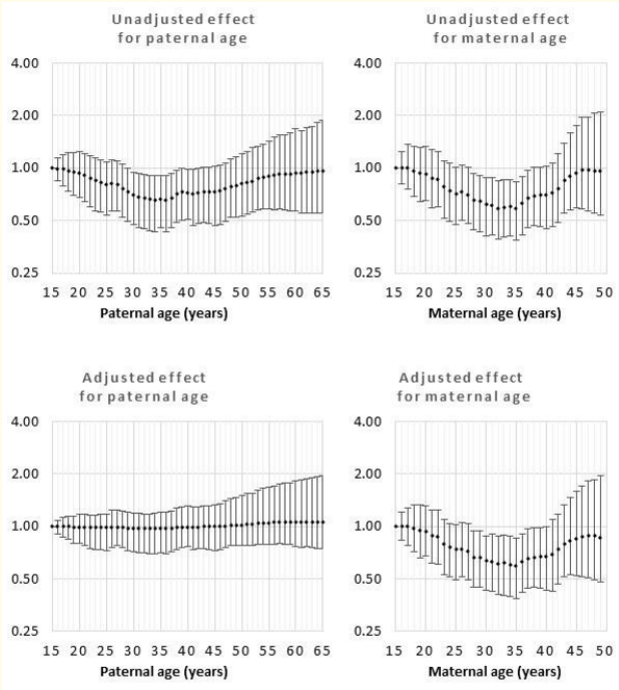
Figure 5: Odds rations for unadjusted and adjusted effects by parent age relative to age 15 years for limb reduction.
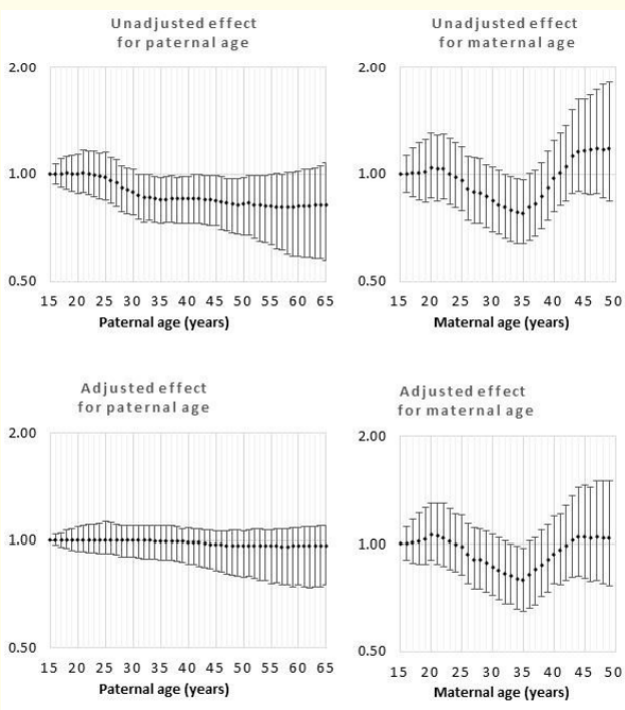
Figure 6: Odds rations for unadjusted and adjusted effects by parent age relative to age 15 years for Cleft lip.
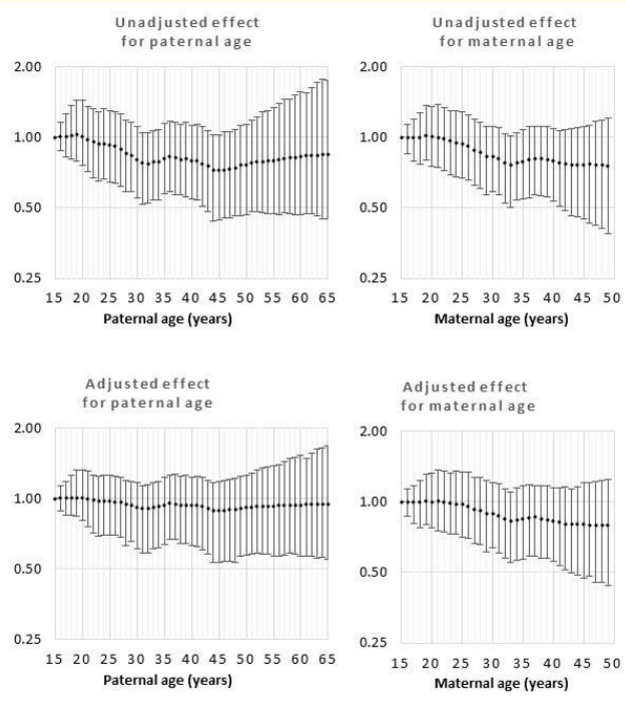
Figure 7: Odds rations for unadjusted and adjusted effects by parent age relative to age 15 years for anencephaly.
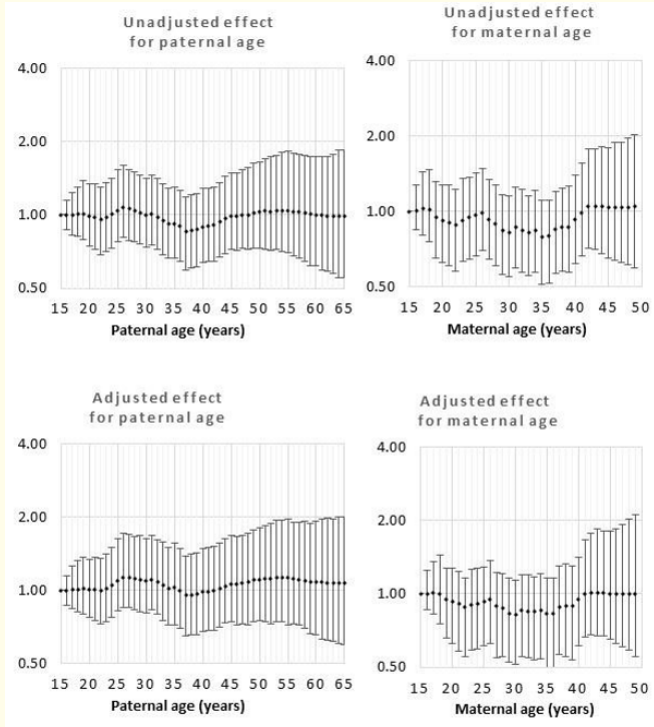
Figure 8: Odds rations for unadjusted and adjusted effects by parent age relative to age 15 years for meningoencephalocele/spina bifida.
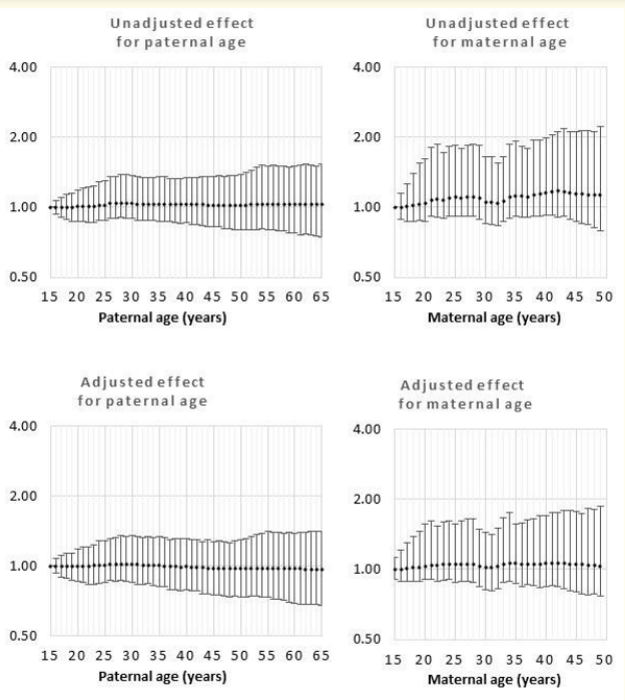
Figure 9: Odds rations for unadjusted and adjusted effects by parent age relative to age 15 years for congenital diaphragmatic hernia.
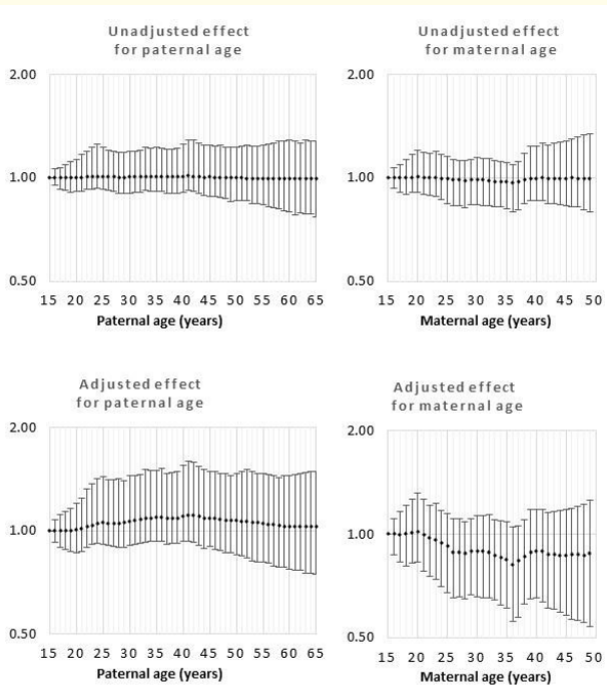
Figure 10: Odds rations for unadjusted and adjusted effects by parent age relative to age 15 years for cleft palate.
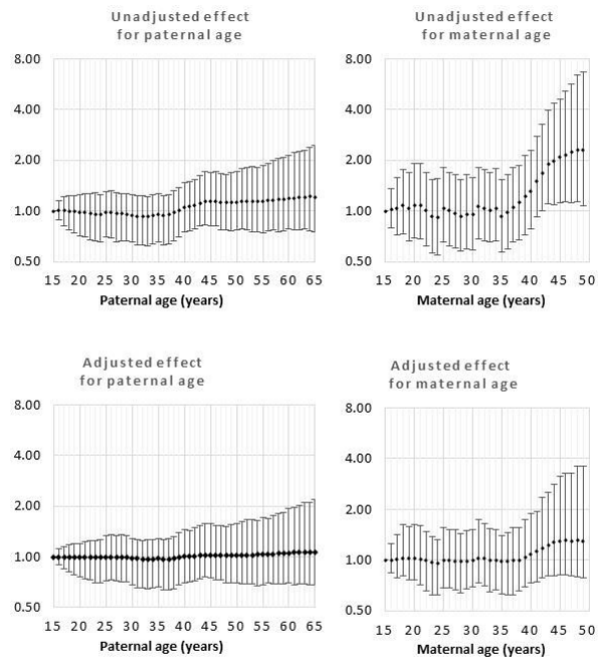
Figure 11: Odds rations for unadjusted and adjusted effects by parent age relative to age 15 years for omphalocele.
This study adds considerable precision and detail to what is known about the risk of parent age on the prevalence of birth defects. The precision results from autoregressive smoothing [12]. When the data are highly correlated, at 1-year age intervals, the gain in precision would be large and when there is no evidence of correlation at 1-year intervals, the risk estimates would be the same as in the model that assumes independence among age groups. Modeling of 1-year age groups, as independent, has been published and showed similar trends but considerably less precision [13]. The precision of year to year effects was not influenced by the diagnostic sensitivity for birth defects. The study utilized NVSS data for all U.S. births for 2014 to 2018. In the 2003 revision of the U.S. Birth Certificate, birth defect recording was restricted to birth defects readily identifiable at birth. Since that time any inaccuracy in recording birth defects has been limited to a low diagnostic sensitivity with no evidence that the misclassification was related to either maternal or paternal age [14]. Simulation analysis showed that for three values of sensitivity, 75%, 50% and 25%, the results for parental age effects on birth defects were virtually identical. Those familiar with the implementation of the CAR model in the BUGS framework may not need this demonstration because the model estimates the log odds for the entire age range constrained to sum to zero and an unconstrained estimate for the intercept [10]. Performing “what-if” scenarios by varying diagnostic sensitivity altered the estimation of the intercept but not the estimates for the 1-year age classifications.
The selection and inclusion of covariates has varied widely among the related research. Much of the existing research adjusted the risks of parent age groups for all covariates without a discussion of how the covariates act as causes. It has been common in the epidemiology literature to reject age as a disease cause because age cannot be prevented. However, adverse birth effects attributed to parent age often result from a decision to delay parenthood [4]. In this instance, applying the backdoor path criterion, confounders of the causal effect of age on BD are possible but they need to be causal to delayed parenting [15]. However, it is more likely that covariates (factors associated with maternal age) are potential mediators and should not be included in the common multivariable approach [16]. For example, any factor acting after fertilization, such as smoking during pregnancy, cannot be a cause of parent age but could be a mediator of a parent age effect. The current approach minimized the inclusion of covariates and guided modeling using a directed acyclic graph (DAG; Figure 12).
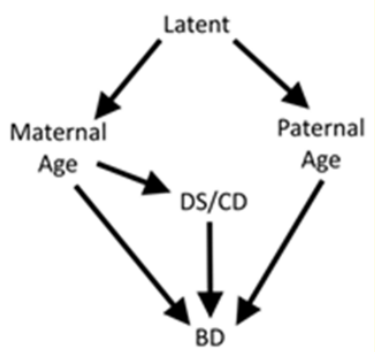
Figure 12: Directed acyclic graph (DAG) used in the study.
Our objective was to provide estimates with a causal interpretation with the potential criticism that potential causes of delayed parenting may be omitted but no mediators would be included in multivariable modeling [15]. The DAG illustrates the modeling assumptions. First, one or more variables cause maternal and paternal ages to be similar. To block confounding between paternal and maternal ages, it would be theoretically possible to block the backdoor path by blocking this variable, if it were known. As an alternative, blocking by maternal age for paternal age and by paternal age for maternal age provides the same control of confounding. Blocking paternal age by maternal age also prevents confounding of the paternal age risk by chromosomal disorders including Down syndrome (CD/DS). A previous study on the same population showed that there was no direct effect between paternal age and CD/DS so CD/DS could confound the relationship but does not mediate paternal age effects [8]. There are options to separate the mediational effects of CD/DS on maternal age including interpretation of the interaction between maternal age and CD/DS [17] but the simplicity of interpreting the effect of maternal age on BD at a single level of CD/DS (i.e. level = absent) was preferred [16]. The importance of these modeling considerations can be seen by comparing the unadjusted and adjusted effects for maternal and paternal age risks for each defect but is most obvious for all defects combined (Figure 1). The unadjusted effect shows a remarkable increase in risk following age 35y for women and a smaller but significant risk starting at age 35y for men. For maternal age, removing CD/ DS and controlling for paternal age produces a very different risk function that is Ushaped with the minimum risk at approximately age 35y and there was no difference in risk between the children of the youngest and oldest mothers. The unadjusted effect for advanced paternal age risk was significant but the estimated risk was very precisely as null (odds ratio = 1) for the entire age range (age 15y - 65y). For paternal age, the difference between the unadjusted and adjusted effects can be explained by the precise controlling for maternal age. The explicit conditions, defined by the DAG, provide a structural approach for investigators to estimate alternative estimates that would be considered “causal” by improving upon the current DAG [15,18]. A better understanding of the biology that constitutes the specific aging effect should be pursued by developing more specific causal models.
Interpretation of adjusted effects showed that risks of increasing maternal age on cyanotic congenital heart disease and hypospadias were small and consistent across maternal ages and similar to those previously reported [2,19-23]. Increased risk of advanced maternal age relative to mid-range maternal age for limb reduction defect [24] and cleft lip [25] have been previously reported but increased risk among the youngest maternal ages and an overall U-shaped risk pattern for these two birth defect classifications is a novel finding attributable to the approach’s strength for modeling non-linear age functions. A very large risk-sparing effect of increasing maternal age on gastroschisis was confirmed and considerable descriptive detail was added for a risk that decreased from age 15 to 49 years [26-29]. Increasing paternal age also had a significant independent sparing risk for gastroschisis. Concern regarding gastroschisis has been increasing because of an unexplained rising birth prevalence of gastroschisis [30,31]. The current results and meta-analysis showed that the odds ratio for the effect of paternal age on all birth defects, combined, was very close to unity. The small difference could be attributed to the inclusion of covariates especially the control of confounding by maternal age. Metaanalysis provided little support for association between increasing paternal age and increasing risk of individual birth defects [6] and based on the simple DAG guiding the current study, increasing paternal age did not cause individual birth defects. These findings have been consistent yet contrast with considerable support for an association between increased germline mutations, evident among older men, and a cluster of adverse birth outcomes claimed to include birth defects [5].
Advancing maternal age was associated with increased birth prevalence of hypospadias and cyanotic congenital heart disease and associated with a lower birth prevalence for gastroschisis. Both older and younger maternal ages were related to limb reduction defect and cleft lip. Advancing paternal age was not associated with an increased birth prevalence of birth defects but was associated with a decreased birth prevalence of gastroschisis.
This research was funded in part by a grant from the National Institutes of Health: R03CA208021.
The author declares that he had no conflict of interest.
Copyright: © 2020 James A Thompson. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
ff
© 2024 Acta Scientific, All rights reserved.