Metin Celalettin1* and Horace King2
1TEPS, Victoria University, Australia
2College of Engineering and Science, Victoria University, Australia
*Corresponding Author: Metin Celalettin, TEPS, Victoria University, Australia.
Received: June 26, 2020; Published: July 30, 2020
Citation: Metin Celalettin and Horace King. “An Electron-based Paediatric Pulmonary Magnetic Resonance Imaging Device to Avoid Administering General Anaesthesia to Paediatric Patients while being Imaged by Exploiting the ‘Celalettin Tunnel Conjecture’”. Acta Scientific Paediatrics 3.8 (2020):56-61.
The ‘Celalettin-Field Quantum Observation Tunnel’ (Celalettin Tunnel) is a quantum observation technique. It is within a pneumatic manifold of Euclidean space where the randomness of particle Orbital Angular Momentum (OAM) is mitigated via electric polarization. It is described by the Celalettin Tunnel Conjecture: The presence of an electric field affects the nuclear spin of the particles within the pneumatic manifold. The manifold, namely the IC-Manifold, or Invizicloud© is unique as its axioms are a combination of classical and quantum non-logical parameters. The IC-Manifold has a variable density and exists only according to ‘Celalettin’s two rules of quantum interaction:
The ‘Celalettin Tunnel Conjecture’ can be exploited to make proposals to ‘Magnetic Resonance Imaging (MRI) machines, such that it could develop an MRI for paediatric use. Paediatric patients are typically administered a General Anaesthesia when undergoing MRI imaging due to the requirement to stay still for extended periods. MRI developed from NMR uses the same phenomena to identify chemical structures based on a spectrum. A technique; in vivo MR spectrograph allows chemical identification on specific parts of the brain. Looking at whether the cells in a brain tumour contain alpha-hydroxy glutaric acid differentiates gliomas that have a mutation in the IDH1 or IDH2 gene for example. Pulse sequences to glean biochemical information non-invasively can be recalibrated for different patients.
In an MRI, the flip angle is the rotation of the nuclear spin vector relative to the main magnetic field. To improve the signal with an MRI, the flip angle needs to be chosen using the Ernst angle. A 90° flip angle using the Ernst angle will yield the maximum signal intensity (or signal-to-noise ratio) per number of averaged Free Induction Decays (FID)s. The flips are done over and over against while the patient stays still, and the average number of nuclear spin ensembles is taken to produce the image. This can involve the patient remaining still for up to five minutes.
This study explores a 180° flip angle could be achieved, then rather than taking several measurements over the fiveminute imaging time experienced by the patient, it could produce a decisive image one measurement. The way to do this would be to focus on the electron rather than the proton. Free electrons are not only aligned with a magnetic field but can be manipulated to be pulled into the direction of the south pole.
Keywords: Celalettin Tunnel; Magnetic Resonance; Anaesthesia
The brain is surrounded by cerebrospinal fluid (CSF), which has roughly the same signal intensity on images as brain tissue. So there a pulse sequence called (fluid attenuation inversion recovery) FLAIR that makes hyperintense signals from water turn hypointense (black) on T2 images while keeping lesions hyperintense and recognisable [11]. This is the same as other tissues in the body; their FLAIR signals are too similar for a single quartersecond image, so multiple investigative techniques are required by the MRI to produce images [10,11]. This weakness in extant MRI technologies causes paediatric patients to be administered a general anaesthesia; a risk that medical practitioners claim outweighs the benefits of diagnostic techniques without an MRI [11,12].
Anti-ferromagnetism affects the OAM spin within the pneumatic matter inside the IC-Manifold [1,2].
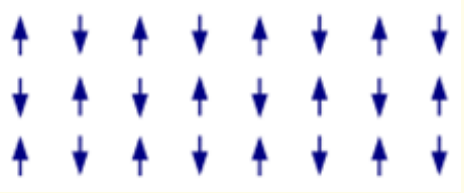
Figure 1: Antiferromagnetic ordering.
The Celalettin Tunnel theoretically works similarly to magnetic resonance imaging [3,4]. An entangled photon depolarizes He-
tunnel [5]. The depolarized particles are considered a single quantum system and can be used to acquire information on the signaller [5-9]. The photon would become weaker as it scattered through an ensemble of atomic Helium-3 until it was absorbed or escaped [10-12].

Figure 2: Celalettin-Field quantum observation tunnel in an IC-Manifold (Helium-3 atoms in grey have been depolarized).
At figure 2, the Celalettin Tunnel is made from the collective depolarized electrons in the IC-Manifold after the signaller has penetrated it [3,5,13,14]. Immediately after the signaller produced a tunnel through the IC-Manifold [5,9,15,16]. If a gas is subject to anti-ferromagnetism its intrinsic spin properties will polarize and portray entropy attributes such like a solid [4,17,18]. Those affected atoms could emit a bound electron depending on the photon’s energy, given:
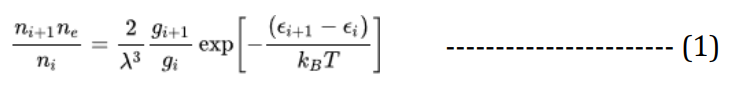
Where:
ni= The density of atoms in the i-th state of ionization, that is with i electrons removed.
gi= The degeneracy of states for the i-ions.
Ei= The energy required to remove i electrons from a neutral atom, creating an i-level ion.
ne= Is the electron density.
λ = The thermal de Broglie wavelength of an electron.
We use the classical models by considering the classical spins with magnetic moments µA 6= µB. To simplify we assume that nuclear spin interaction is disordered of the Heisenberg form [9,22,23,27]. So, the ferromagnet model described by the classical Hamiltonian of the type:
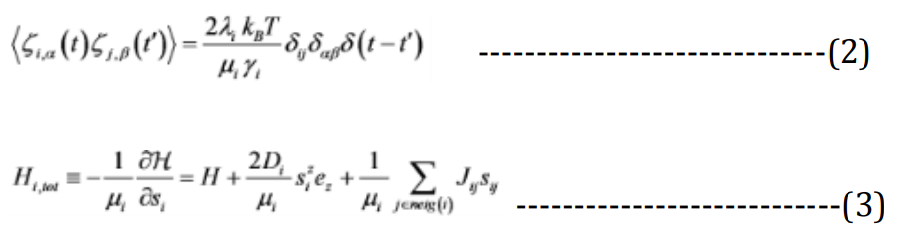
Where:
H = Hamiltonian
N = Total number of spins
I and J = Lattice sites
Di = The anisotropy constant of site I
|Si | = 1 The third sum is over neighbour pairs
Jij = JAA(BB)>0 Heisenberg exchange interaction parameter
λi = Is the coupling to the heat bath parameter
a,B = Cartesian Z components heat bath and T is the temperature.
Each point of an n-dimensional manifold has a neighbourhood or a set of points acting like barriers, defining the region where the content within the IC-Manifold can exist, or the walls of the IC-Manifold itself [17] [24]. Helium-3 has an intrinsic nuclear spin of ½ and can be hyperpolarized by spin exchange optical pumping. Depolarization occurs to make way for the quantum entangled photon [4]. Hyperpolarization using non-equilibrium means for spin-exchange optical pumping is achieved by Coulomb Forces; such that:

Where:
r = The distance between the two charges q and Q Newtons.
Given the Boltzmann equation to accommodate the density of the environment in which the photon-electron interactions will occur in the presence of an electric field:
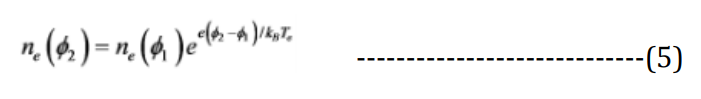
Where:
ne = Electron number density
Te = Temperature of the plasma, and
kB = Boltzmann constant.
φ = Work function.
Fluid attenuation inversion recovery in paediatric ‘Severe Acute Respiratory Syndrome Coronavirus-2’ (COVID-19) patients.
MRI developed from NMR uses the same phenomena to identify chemical structures based on a spectrum [1,2,11]. A technique; in vivo MR spectrograph allows chemical identification on specific parts of the brain. Looking at whether the cells in a brain tumour contain alpha-hydroxy glutaric acid differentiates gliomas that have a mutation in the IDH1 or IDH2 gene for example. Pulse sequences to glean biochemical information non-invasively can be recalibrated for different patients [11,12].
In an MRI, the flip angle is the rotation of the nuclear spin vector relative to the main magnetic field. To improve the signal with an MRI, the flip angle needs to be chosen using the Ernst angle:

A 90° flip angle using the Ernst angle will yield the maximum signal intensity (or signal-to-noise ratio) per number of averaged Free Induction Decays (FID)s. The flips are done over and over against while the patient stays still, and the average number of nuclear spin ensembles is taken to produce the image [1,2,11]. This can involve the patient remaining still for up to five minutes.
If a 180° flip angle could be achieved, then rather than taking several measurements over the five-minute imaging time experienced by the patient, it could produce a decisive image one measurement. The way to do this would be to focus on the electron rather than the proton. Free electrons are not only aligned with a magnetic field but can be manipulated to be pulled into the direction of the south pole [11,12].
If the electron were pulled at a 180° flip angle in an MRI, then the patient would be exposed to a length of time of imaging in the diagnostic of ‘Severe Acute Respiratory Syndrome Coronavirus-2’ comparable to a handheld ultrasound or a CT. The electromagnetic strength required is given by Faraday’s law of induction. The trajectory of an ensemble of particles is derived from the Lagrange equations, where the Euler-Lagrange equation describes the motion for the scalar field [1].
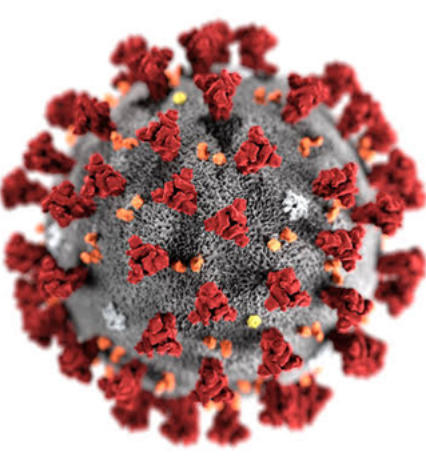
Figure 3: ‘Severe Acute Respiratory Syndrome Coronavirus-2’ (COVID-19).
A paediatric patient suffering ‘Severe Acute Respiratory Syndrome Coronavirus-2’ (COVID-19). It infects and damages the type II alveolar cells of the lungs. Common symptoms include fever, cough, and shortness of breath. While chest CT is considered the modality of choice to diagnose pulmonary damage, such scans aren’t always as conclusive as an MRI [11].
As an alternative, bedside lung ultrasound is frequently used as a diagnostic. As the global infection rates of COVID-19 continue to rise, investigators in Italy evaluated whether lung ultrasound could be an effective tool in also identifying patients who have pneumonia specifically associated with the virus. The results weren’t significant. However, since its inception, the MRI has been the Rolls Royce of diagnostic imaging [3-5,11,12].
For an adult, it would be unlikely that they would need an MRI as a CT scan would be sufficient, however in a paediatric patient where complications of Covid-19, pneumonia and other respiratory conditions, it may be too difficult to use these techniques. To determine whether ultrasound could feasibly be used to pinpoint COVID-19 pneumonia, researchers analysed 12 emergency department patients with the COVID-19 infection. These individuals received both lung ultrasound and CT. CT scans correlated strongly with the ultrasounds. 12 patients had ground-glass opacity; five patients had a crazy-paving pattern. Scans identified a diffuse Bpattern with spared areas in all patients, and only three had posterior subpleural consolidations. The research showed that using a hand-held ultrasound was about as effective as a CT scan, where in the past, CT scans were the standard protocol for COVID-19 diagnostics.
In an IC-Manifold, the Celalettin Tunnel is theoretically produced by an incoming entangled photon. When viewed as a single quantum system, the collectively affected Helium-3 atoms describe the photon.
The Schrodinger wave function equation:
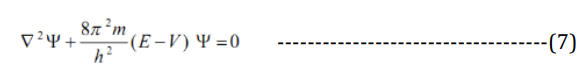
Where the Laplacian of a scalar for spherical coordinates is given by:
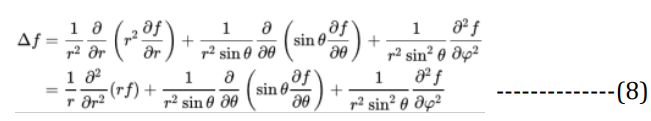
Where:
E = Energy
V = Potential Energy
m = Mass
h = Planck’s constant
φ = The azimuthal angle, and
θ = The zenith angle or co-latitude.
Rearranged to express quantum entangled photons:
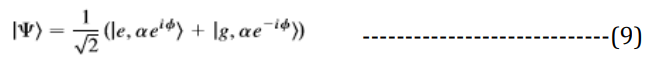
Where:
αe = Eigenvalues
e = γsig
g = γidler.
An electron’s spin: |↑|↑
With an observer: |↑|obs|↑|obs
For an entangled quantum system: |↑⟹(|→+|←)/2– √|↑⟹(|→+|←)/2
Where the observer is added: |↑|obs⟹(|→+|←)|obs/2– √|↑|obs⟹(|→+|←)|obs/2.
If the observer can measure the state, then the state of the observer changes and the observer can no longer be factored out of the whole state: (|→|obs1+|←|obs2)/2–√(|→|obs1+|←|obs2)/2. The quantumness of |obs1≠|obs2|obs1≠|obs2 describes the electron spin as not acting quantum mechanically and hence decoherence is achieved [25].
Spin exchange optical pumping can be represented by:
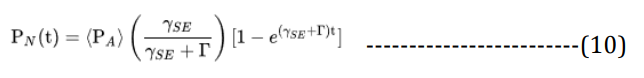
Where:
PN(t) = Nuclear polarization (spin)
(PA) is the atom’s polarization
γSE = The spin exchange rate
Γ = The longitudinal relaxation rate.
The Lagrangian scalar formulation to investigate the required kinetic energy of a photon to cause the Celalettin Tunnel [24]. It is given by:
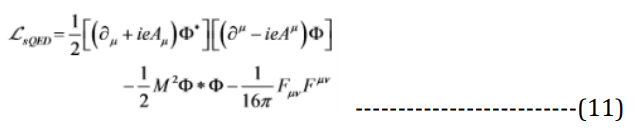
Where:
Φ = Charged scalar field,
Φ∗ = Its complex conjugate.
The electromagnetic strength required is given by Faraday’s law of induction. The trajectory of an ensemble of particles is derived from the Lagrange equations, where the Euler-Lagrange equation describes the motion for the scalar field [1]:

Yielding the Klein-Gordon [15]
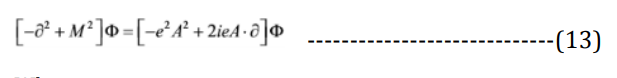
Where:
∂2 ≡ ∂µ∂µ,
A2 ≡ AµAµ
A·∂ ≡ Aµ∂µ
Further,
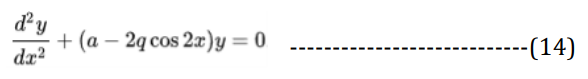
Where:
a and q are the quantum parameters.
That is repolarizing the Celalettin Tunnel within the IC-Manifold. That time is expected to occur, given:

Where:
Mxy= the transverse component of the magnetization vector
T2= a time constant characterizing the signal decay
e= Euler’s number.
A ‘Celalettin Tunnel Conjecture’ can therefore mathematically be described:
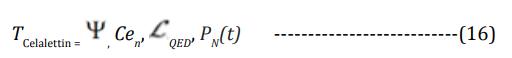
Where:
TCelalettin is the Celalettin Tunnel
Cen is the Mathieu differential equation
LQED symbolizes Lagrangian QED
PN(t) is the rate of nuclear spin repolarization.
While the Celalettin Tunnel Conjecture exploits antiferromagnetism to manipulate particle spin, it can be used on free electrons in paediatric patients, and if pulled at a 180° flip angle in an MRI, then the patient could be exposed to a length of time of imaging in the diagnostic of ‘Severe Acute Respiratory Syndrome Coronavirus-2’ comparable to a handheld ultrasound or a CT. This would avoid the need to administer General Anesthesia to paediatric patients undergoing pulmonary imaging for COVID-19 diagnostics.
Copyright: © 2020 Metin Celalettin and Horace King. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
ff
© 2024 Acta Scientific, All rights reserved.