Teruo Mori1*, Munenori Noda2, Yoshiyuki Iwanaga3, Soichiro Tanabe4, Ryousuke Fujimoto5, Izuru Sadamatsu6 and Keiichi Ikeda7
1 Mori Consulting Office, Shizuoka Japan
2Toyoda GOSEI Ltd, Aichi Japan
3Shikoku Poly Tech College, Kagawa, Japan
4Chuo University, Tokyo, Japan
5Shibaura Machine Ltd, Shizuoka, Japan
6 Team SHIZUOKA for OPTIMIZING, Miyagi, Japan
7DAICEL CORPORATION, Hyogo, Japan
*Corresponding Author: Teruo Mori, Mori Consulting Office, Shizuoka Japan.
Received: May 23, 2024; Published: August 13, 2024
Citation: Teruo Mori., et al. “Conference matrices C4, C6, C8: Expanding Matrices Changing the Element Layout Structure to easy Operation". Acta Scientific Nutritional Health 8.9 (2024):21-24.
A conference matrices has the diagonal as "0", the 1st row and 1st column as "1", and the other parts as "-1" and "1". Let's call the former the core (CORE) and the latter the body (A). By changing the positive and negative values of the core and body, they maintain also orthogonal as matrices that are easy to layout. They can accommodate the various levels of experimental design by researchers.
Keywords: Conference Matrices; Optimizing; Analysis; DOE; Taguchi Methods
There was the Taguchi design of experiments based on the mixed type orthogonal table and evaluation with SN-ratio [1]. However there were the fatal problems that were to request too much number of trails and poor estimations for optimum condition s by selecting the factor effect charts. The researchers have been expect to improve those kinds of the fatal defects of Taguchi methods [1]. Actually, the optimum conditions with 62% [2] cases studies optimizing by Taguchi methods were under the top of response value data at orthogonal array table L18. So, the 62% optimums were not over the top of trial values of the L18 orthogonal Table results. we have been conducted the New WAY:C [a, b] design [3] to reduce the number of experiments with C matrices and to get the better estimation with [a, b] analysis to detect the interaction for layout factors.
There was the Taguchi design of experiments based on the mixed type orthogonal table and evaluation with SN-ratio [1]. However there were the fatal problems that were to request too much number of trails and poor estimations for optimum condition s by selecting the factor effect charts. The researchers have been expect to improve those kinds of the fatal defects of Taguchi methods [1]. Actually, the optimum conditions with 62% [2] cases studies optimizing by Taguchi methods were under the top of response value data at orthogonal array table L18. So, the 62% optimums were not over the top of trial values of the L18 orthogonal Table results. we have been conducted the New WAY:C [a, b] design [3] to reduce the number of experiments with C matrices and to get the better estimation with [a, b] analysis to detect the interaction for layout factors.The most popular C matrices [4] are C4, C6, C8. We show C4 matrices to table 1. New WAY:C [a, b] will be applied Belevitch [5] type C matrices.
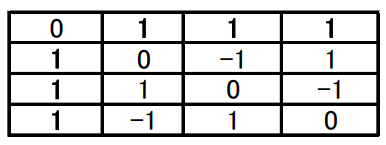
Table 1: C4(2133).
The C matrix satisfies the following three requirements.
1: The diagonal component is ``0''.
2: Each element is either ``-1'' or ``+1.''
3: Each column is orthogonal
When applying the C matrix, the column elements [-1,0,1] are replaced with the ``1st, 2nd, and 3rd'' levels.
The order of allocation levels is often set according to the trends of (small, medium, and large), (short, medium, and long), and (weak, medium, and strong) and etc.
Therefore, when the C matrices is applied to the design matrices, the third level is gathered in each column of the first row.
Comparing the current Hadamard matrices (L8, L27), which consists of the first row with the first level, and the mixed system orthogonal array (L18, L36), it was evaluated as lacking in convenience.
There were many requests from researchers to make the first level the first row in order to make the C matrices as friendly design matrices. Of course, there was a proposal from the matrices research side to replace [-1, 0, 1] in Table 1 with the "3rd, 2nd, 1st" level. However, researchers at the design site said, ``This proposal can be assumed to be prone to errors.'' We promised to conduct the countermeasure to research C matrices generation to meet this requests.
Therefore, we generated C matrices with the different arrangement of elements, with the core (CORE) and body (A) signs changed to positive or negative.
The generation mechanism of the C matrix is shown. The Legendre index is shown in table 2. p is a prime number and a is an integer.
Let's take an example of p=5. Since p is 5, squaring 1, 2, 3, and 4 gives 1, 4, 9, and 16. When dividing this by p (5), the remainder is 1 ,4,4,1.
Since both remainders 1 and 4 remain, if we set 1 and 4 of integer to [1], 2 and 3 of integer to [-1], and 0 to [0], and position them at the beginning. [0,1, -1, -1, 1] is the Legendre index of p5.

Table 2: Legendre symbol.
The Legendre indices p5 are combined vertically and moved horizontally, one by one, in five columns as shown in table 3. Table 4 shows the obtained 5 rows and 5 columns (BODY) within the square frame. Note that this generated matrices is composed of the cyclic matrices.
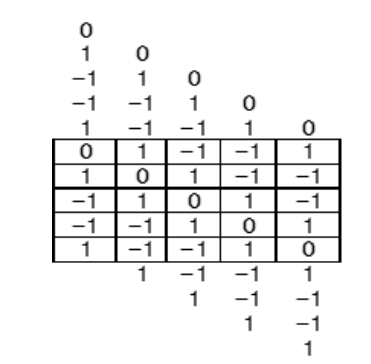
Table 3: 5 rows with p5 shifted by one.
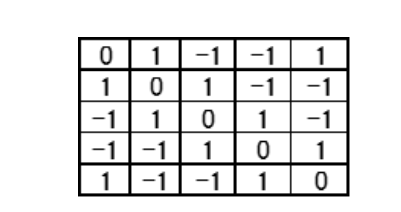
Table 4: Obtained matrices (BODY).
Add ``0'' to the top left of Table 4 and place ``1'' in the first row and first column, as shown in the completed table 5.
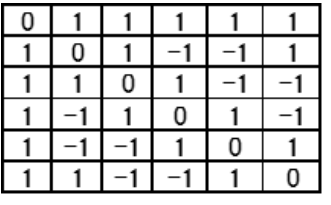
Table 5: Completed C6 (2135) (T).
Table 6 shows the transposed matrices T', the original T', and the product T'T is shown in Table 7. The diagonal components are 5, and other elements are ``0''.
We confirmed the element of Table 5 Orthogonality between each layout factors.
The above describes the C matrices generation method implemented by Belevitch.
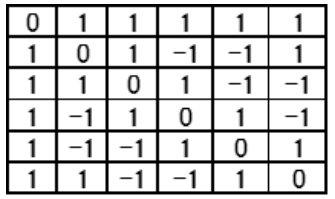
Table 6: Transposed matrix (T’).
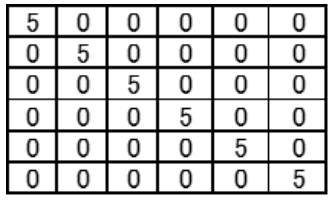
Table 7: Product T’T: Confirmation Orthogonality
C matrices researchers Balonin and Jennifer [3] defined the Belevitch matrices as shown in Table 8, where BODY is A and the matrices [1,1,1,….] is (e,eT).
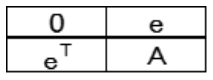
Table 8: Definition of Belevitch matrices by Balonin and Jennifer.
The definition in Table 8 is the Belevitch-type with 6 rows and 6 columns, where e, eT, and A are positive (+).However, we confirmed that orthogonality was maintained even when the positive (+) of each term was individually changed to negative (-).
The confirmation of the orthogonality of the corresponding C4(2133) matrices with "eT" ⇒"-eT" confirmed here is shown below. The definition of "eT" ⇒ "-eT" is shown in table 9, the C4(2133) matrices is shown in Table 10, the transpose T' is shown in table 10, and the product T'T is shown in table 11. In table 11, the elements outside the diagonal are ``0'', so Table 10 of the design matrices is orthogonality defined at table 9.
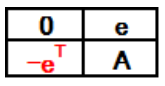
Table 9: Definition of “eT” ⇒ “-eT”.
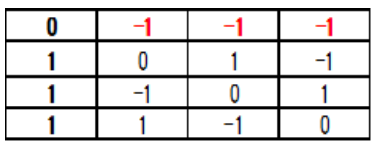
Table 10: Transposed matrices T’.
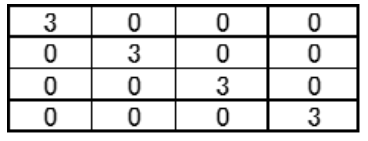
Table 11: Product T’T: Confirmation Ortogonality.
We showed the C4(2133) matrices under changing `A'' ⇒ ``-A'' and confirmed orthogonality of it. The definition of ``A'' ⇒ ``-A'' is shown in table 12, the C4(2133) matrices is shown in table 13, the transpose T' is shown in table 14, and the product T'T is shown in Table 16. In Table 15, all the columns except the diagonal are 0, and the columns are orthogonality.
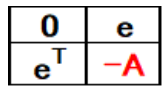
Table 12: Definition of “A” ⇒ “-A”.
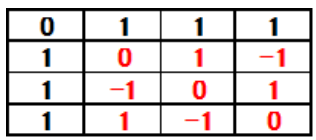
Table 13: A⇒-A:C4(2133) Matrices.
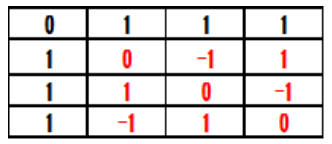
Table 14: Transposed Matrices (T’).
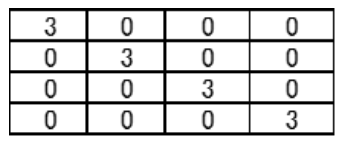
Table 15: Product T’T: Confirmation Orthogonality.
The researchers will cover all subjects with almost three kind C matrices C4, C6, and C8. For this reason, we limited them in C4, C6, and C8 and generated C matrices with different element arrangements by reversing the positive/negative of the core [e, eT] and the body [A] of the Belevitch type matrices. We could confirm Orthogonality between columns even if each terms in the core and body were individually reversed. We reversed the positive and negative definitions of [e,eT] and [A] . We generated C4 matrices are shown in Table 16-1/2, the C6 matrix is shown in Table 17-1/2, and the C8 matrices is shown in Table 18-1/2.
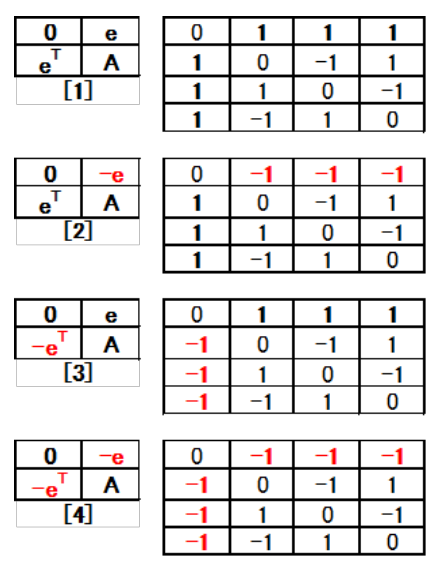
Table 16: 1 C4 (2133) core positive and negative at A (+).
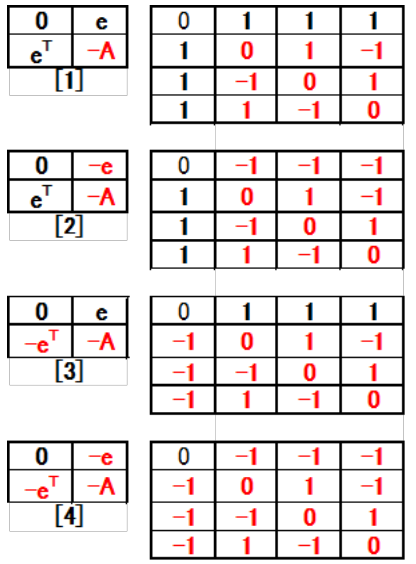
Table 17: 2 C4 (2133) core positive and negative at A (-).
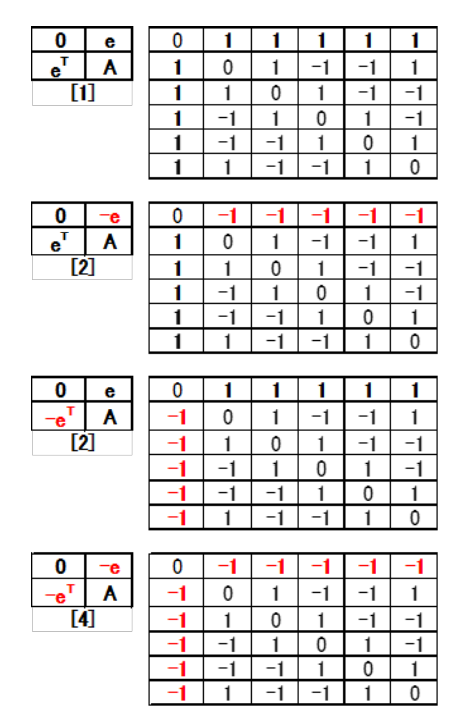
Table 18: C6(2135) core positive and negative at A(+).
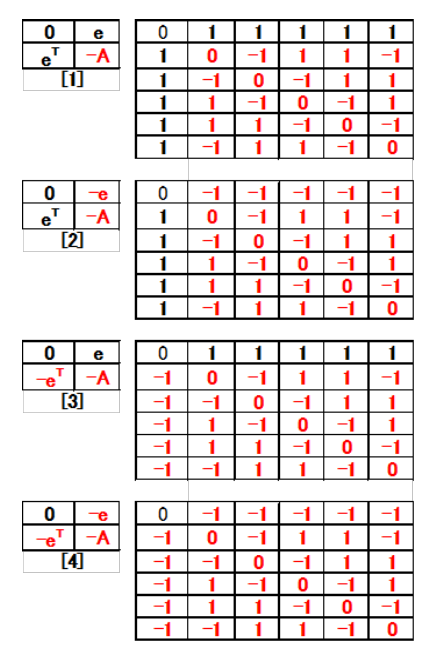
Table 18-2: C6(2135) core positive and negative at A (-).
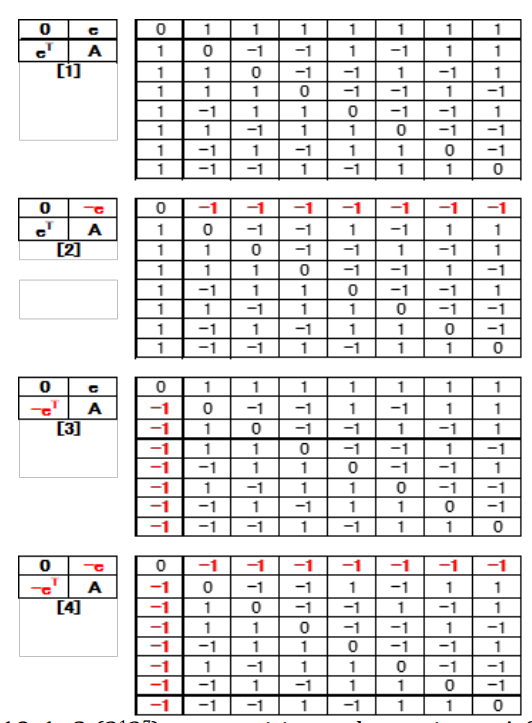
Table 19-1: C8(2137) core positive and negative at A (+).
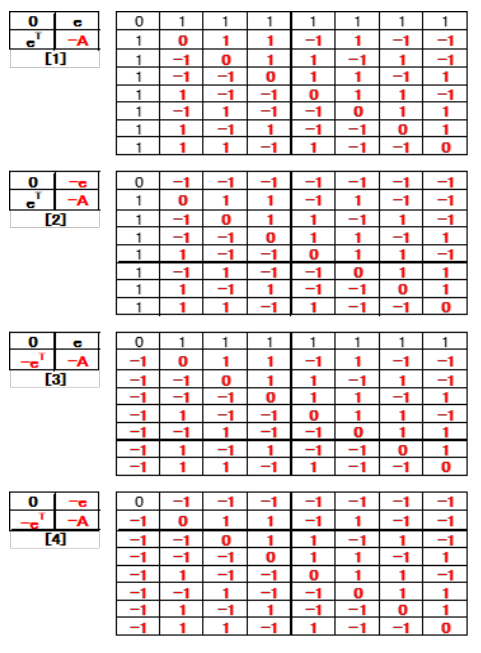
Table 19-2: C8(2137) core positive and negative at A (-).
The description of the transposed matrix T' and the product T'T is omitted, but orthogonalities have been confirmed.
We expect they will contribute to optimize the researcher subjects with 1/3-1/2 to Taguchi way L18.
Copyright: © 2024 Teruo Mori., et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.